Relatório 22- Relações trigonométricas no triângulo retângulo

História:
A trigonometria apareceu por volta do século IV a.C, através dos egípcios. Muitas pessoas dizem que o seno, o cosseno e a tangente tenham aparecido para resolver alguns problemas gerados pela astronomia.
Conteúdo:
Seno de um ângulo agudo :

 
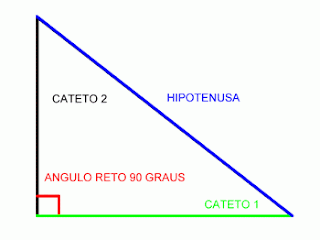
O seno é sempre a razão entre a medida de um cateto oposto e a medida da hipotenusa.
Nesse caso queremos descobrir o seno de x então fazemos 5 sobre 11 que será igual a medida do seno.
Cosseno de um ângulo agudo:

O cosseno é o que complementa o seno, então para calcular usamos a medida do cateto adjacente dividido pela hipotenusa.
Tangente de um ângulo agudo

Para calcular a tangente basta fazer o cateto oposto dividido pelo cateto adjacente
Tabela trigonométrica

Para calcular o seno e o cosseno utilizamos essa tabela ou uma calculadora científica.

 
Razões trigonométricas dos ângulos notáveis
Nós temos que usar essa tabela para calcular o seno,cosseno e a tangente dos ângulos de 30º, 45º e 60º

 

 
E fazemos essas operações para descobrir esses números.
Principais dificuldades:
Eu não entendi muito dessa matéria só consegui aprender o básico e estou errando os exercícios e deixando muitos em brancos porque a minha dificuldade é saber calcular com a tabela trigonométrica e é também calcular o seno,cosseno e tangente de 30,45 e 60 pois não consigo fazer essas operações com raízes,mas eu acho que se eu estudar e tentar tirar minhas dúvidas consigo entender melhor.

Exercícios que não resolvi:

p.147 ex 7,8 e 9
p.153 ex: 5,6,10,11,12,13,14,15,16,17,18,19,20,21- pois não entendi nada que tinha que fazer .

Relatório 21 – Outras relações métricas no triângulo retângulo

Relações métricas:

1º Para descobrir a hipotenusa

Esse é fácil só basta aplicar o teorema de Pitágoras !

Definição:

Num triângulo retângulo qualquer a soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.

2º Para descobrir a altura relativa:

Temos que usar a fórmula:

b.c = a.h

Definição:

Num triângulo retângulo qualquer o produto das medidas dos catetos é igual ao produto da medida da hipotenusa pela medida da altura relativa à hipotenusa.

3º Para descobrir os catetos

Temos que usar a fórmula com as projeções ortogonais:

b²=  a·n

c²= a·m  

Não se deve fazer o teorema de Pitágoras inverso !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Definição:

Num triângulo retângulo qualquer,o quadrado da medida de um cateto é igual ao produto da medida da hipotenusa pela medida da projeção ortogonal desse cateto sobre a hipotenusa.

4º Para descobrir o quadrado da altura relativa:

h²= m·n

Definição:

Num triângulo retângulo qualquer,o quadrado da medida da altura relativa à hipotenusa é igual ao produto das medidas das projeções ortogonais dos catetos sobre a hipotenusa.

Principais dificuldades:

É calcular números x com operações usando os radicais exemplo 2√3 e também não consigo resolver problemas sem desenho geométrico mas estou entendendo a matéria.

Exercício que não resolvi.

p.135 ex: 5 e 7

Relatório 20 -Teorema de Pitágoras

 
História:

• Pitágoras viveu no séc. VI a.C., na Grécia e pensa-se que nasceu na ilha de Samos;
• Diz-se que Pitágoras viajou pelo Egito e pela Babilonia vindo a fixar-se no sul da Itália (em Crotona) fundando a chamada Escola Pitagórica, onde se estudava Matemática, Filosofia, Música e outras Ciências;
• Foi Pitágoras o primeiro a elevar a ciência dos números e da geometria à categoria das artes maiores e a estabelecer o princípio de que uma proposição científica deve ser totalmente convincente, isto é, verdadeiramente demonstrada;
• Atribuem-se notáveis descobertas a Pitágoras, tais como o sistema de numeração decimal, tabelas de multiplicação e a demonstração do célebre teorema que leva o seu nome;
• Há uma lenda que conta que Pitágoras ofereceu aos deuses mil bois como agradecimento, por ter descoberto a demonstração do referido teorema;
• Os Pitagóricos tinham algumas superstições e para prevenir desgraças usavam o símbolo «pentagrama», nas portas das casas e nos sítios que queriam preservar de maus acontecimentos;
• Este teorema indica que os gregos conseguiram estabelecer uma ligação abstracta entre os números e as figuras, o que representa um importante esforço intelectual. Também prova que tinham aprendido a demonstrar, e não apenas a persuadir, o que representa um considerável salto cognitivo.
• Existem inúmeras demonstrações do teorema de Pitágoras. Em 1940 o matemático americano Elisha Scott Loomis compilou 367 demonstrações diferentes para o seu livro 'The Pythagorean Proposition';

Explicação do teorema:

Pitágoras diz que em qualquer triângulo retângulo a soma das medidas dos catetos elevados ao quadrado é igual ao quadrado da hipotenusa.

 

 

Exercícios que não resolvi:

p.130 ex 9

Relatório 19-Casos de Semelhança

Casos de Semelhança

1º Caso: Ângulo- Ângulo

É quando dois triângulos têm dois ângulos internos correspondentes congruentes.

   

- Então o triângulo AGH é congruente ao triângulo DEF.

- Ângulo A é congruente ao ângulo D.

 - Triângulo AGH é semelhante ao triângulo ABC.

Por isso concluímos que o triângulo ABC é congruente ao triângulo DEF.

2º Caso: Lado-Ângulo-Lado

É quando as medidas de dois dos lados de um triângulo são proporcionais aos do outro triângulo e os ângulos determinados por estes lados são congruentes, então os triângulos são semelhantes.

3º Caso: Lado- Lado- Lado

 Se todos os lados de um triângulo forem proporcionais aos lados de outro, os dois triângulos são semelhantes.

                                                                                                                                             

Principais dificuldades:

É descobrir o valor de x em problemas com esses triângulos.

Exercícios que não resolvi.

 p.123 ex 8

Relatório 18 - Triângulos Semelhantes

Triângulos Semelhantes

De acordo com a semelhança de triângulos eles são semelhantes se:

-Seus ângulos correspondentes  são proporcionais.

 -Os lados corespondentes são proporcionais.

Teorema Fundamental da Semelhança de Triângulos:

 

 Quando qualquer reta interceptar um triângulo então o triângulo que ela determina é semelhante ao primeiro triângulo da figura.

Principais Dificuldades:

Resolver alguns exercícios em que aparecem Triângulos juntos à paralelogramos.

Exercícios que não resolvi:

P.119 ex: 5 e 8

Relatório 17 - Propiedade dos polígonos semelhantes

Razão entre perímetros:


Se há dois poligonos semelhantes a sua razão de semelhança será igual a razão de seus perímetros.
veja o exemplo:

então a + b + c + d +e +f  dividido por G+H+I+J+K+M será igual à E dividido por K.




Razão entre áreas


Se há dois polígonos semelhantes a razão entre suas áreas será simplesmente elevada ao  quadrado.

Principais dificuldades:


É descobrir a semelhança de áreas de retângulos em problemas.


Exercícios que não resolvi:
p.116 ex 2 e 3

Relatório 16 - Aplicando o Teorema de Tales

Definição:

Quando uma reta paralela à um lado de um triângulo intercepta os outros dois lados em dois pontos distintos,ela determina sobre esses lados segmentos proporcionais.

Resumo do conteúdo:

Pelo teorema de Tales é posível afirmar que a medida de um lado é proporcial à medida do outro lado.veja o exemplo:

Usamos AD/BC = AE/EC

Para descobrir o valor do x calcula-se 8/x = 10/2 e podemos usar a multiplicação em cruz.

                                                            

                                                            16=10x

                                                             x=6

2º CASO

Definição:

A bissetriz de um ângulo de um triângulo divide o lado oposto a esse ângulo em dois segmentos proporcionais aos lados adjacentes a esses segmentos.

Resumo do Conteúdo:

  Quando há bissetriz no triângulo aplicamos AB/BD = AC/DC

Principais Dificuldades:

É calcular quando há ângulos dentro do triângulo e também é calcular quando há números decimais dentro do triângulo .

Exercícios que não resolvi:

p.107 ex 8,9 e 10.